Accueil > 02 - SCIENCES - SCIENCE > Atome : La rétroaction de la matière/lumière et du vide (de la (...) > « Comment un observateur se déplaçant à la vitesse de la lumière (aux (...)
« Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte
samedi 2 février 2019, par

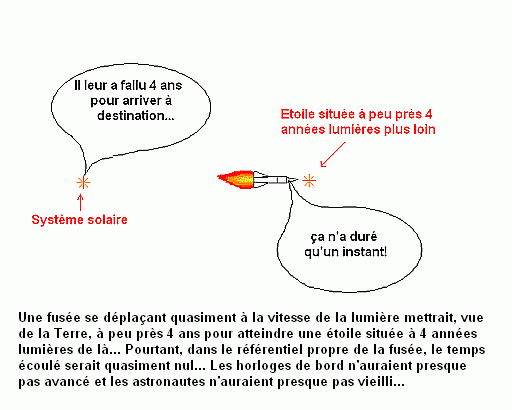
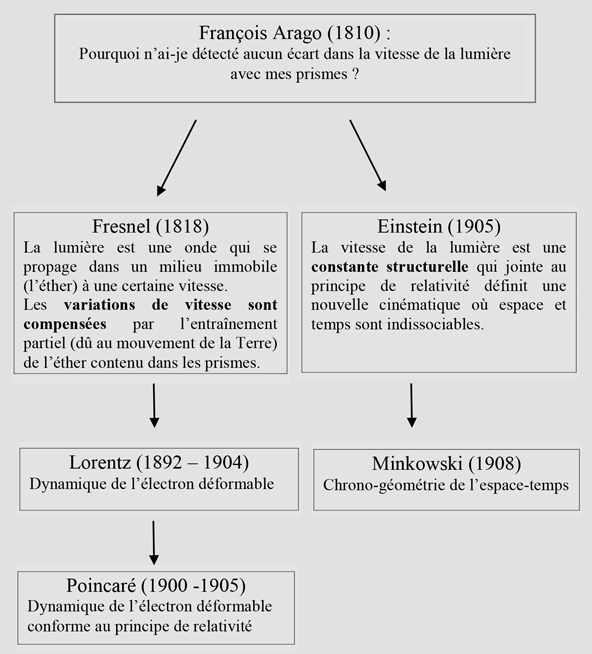
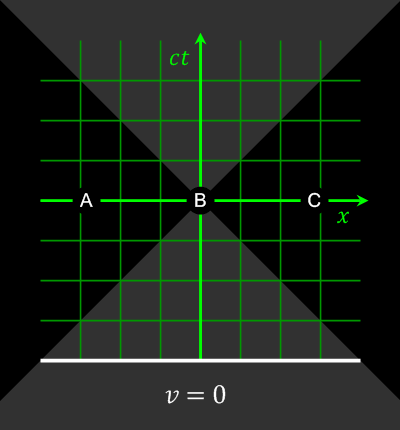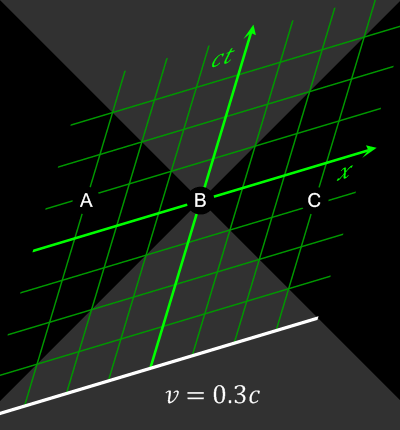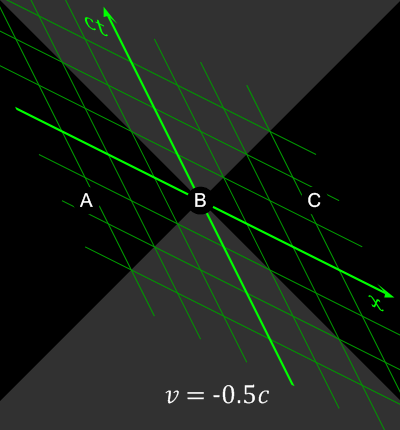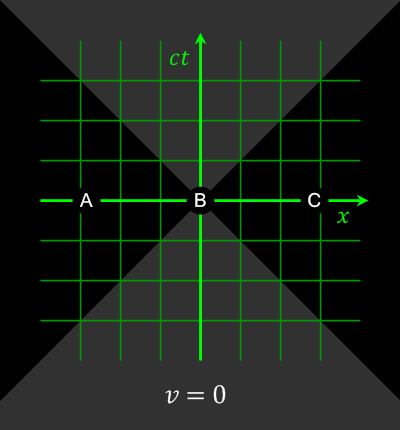
Le paradoxe de la relativité restreinte d’Einstein : « comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? »
Quels problèmes pose cette simple question naïve qu’Einstein s’est posée à l’âge de seize ans ?
Eh bien, elle pose le problème à la fois de la vitesse constante de la lumière et celle des conceptions de la mécanique. Et c’est un véritable paradoxe car les deux sont apparemment diamétralement opposés. En fait, ils vont s’avérer seulement dialectiquement opposés.
Le paradoxe d’Einstein sur la relativité peut s’énoncer ainsi :
« La vitesse d’un corps en mouvement est relative et la vitesse de la lumière est absolue… »
Einstein devait répondre ainsi : toute vitesse est intrinsèquement reliée à la vitesse de la lumière (qui est la vitesse de toutes les interactions, celles-ci n’étant jamais instantanées, même si elles sont très rapides : 300.000 kilomètres par seconde !) et, par conséquent, quand la vitesse augmente, elle est de plus en plus bornée par la vitesse de la lumière (cette résistance du vide est indiquée par l’augmentation de la masse inerte).
Les deux principes de la relativité restreinte (première loi : une loi valable dans un système inertiel l’est dans tout autre système inertiel ; deuxième loi : la vitesse de la lumière est indépendante de la vitesse de sa source et du système de coordonnées) sont apparemment contradictoires bien que tous deux vérifiés expérimentalement et c’est là que réside le paradoxe d’Einstein de la relativité restreinte, paradoxe dont il devait montrer qu’il ne se résout pas en détruisant l’une des hypothèses mais en montrant que ces contraires ne sont pas dichotomiques mais interactifs et interdépendants. On peut lire ici en quoi la théorie de la relativité introduit une dialectique dans la physique
Plusieurs points ont dû être modifiés de manière révolutionnaire en physique pour y parvenir, à commencer par la fixité de la masse et, plus généralement, par la transformation de la notion d’inertie et d’énergie et de leurs liens contradictoires.
L’idée d’un objet accompagnant un rayon lumineux a due être abandonnée puisqu’aucun corps matériel (possédant une masse inerte) ne peut s’approcher de la vitesse de la lumière sans voir sa masse devenir infinie !)
Le photon, corpuscule lié à la lumière et au rayonnement plus généralement, n’est pas un objet fixe mais une dynamique des structures du vide quantique issue des paires électrons-positons, c’est-à-dire de couples matière-antimatière.
On peut penser que le photon ne devrait pas être appelé corpuscule, ce terme étant réservé à la matière. Mais, en fait, le photon peut devenir matériel dans certaines circonstances… Le photon se transforme alors en particules massives.
Si, comme on le croyait, la lumière était une vibration électromagnétique dans l’éther semblable aux ondes sonores vibrant dans un milieu matériel, l’air, la lumière se propagerait avec une vitesse relative par rapport au vide, une vitesse de 300.000kilomètres par seconde. Mais une telle image, celle des ondes sonores par exemple, entraînerait des bizarreries impossibles. Ainsi, on ne pourrait pas regarder l’image de ce photon lumineux en déplacement dans un miroir. Pour aller au miroir, la lumière devrait aller à la même vitesse que le photon et elle ne pourrait pas être réfléchie. On ne peut pas raisonner sur quelque chose se déplaçant à la vitesse de la lumière comme on raisonne sur un objet, sur une chose. Cela rejoint d’ailleurs un peu les leçons que l’on peut tirer de l’expérience de Young : on ne peut pas raisonner sur les corpuscules de matière et de lumière comme s’il s’agissait d’une chose, unique, précise, toujours identique à elle-même.
Curieusement, la relativité en physique provient de deux absolus, c’est-à-dire qui ne dépendent ni de l’observateur ni de l’émetteur du phénomène, ni de sa nature, ni de son mouvement. Ces deux absolus sont les lois de la physique et la vitesse de la lumière. Tous deux sont indépendants de l’observateur, de sa nature et de son mouvement rectiligne uniforme, de l’émetteur, de la source du phénomène.
C’est pour préserver ces deux absolus que la relativité nouvelle, celle d’Einstein, va admettre comme relatifs, c’est la masse, l’espace, le temps.
Le mouvement des objets est-il relatif ou absolu ? Est-il seulement détectable par un observateur qui ne subit pas ce mouvement ou l’est-il aussi de l’intérieur ? Les phénomènes internes de l’objet (comme électromagnétisme, gravitation, etc.) peuvent-ils permettre de détecter ce mouvement ou faut-il la comparaison avec un autre objet à l’extérieur ? Cela signifie : le mouvement modifie-t-il le phénomène intérieur au point de permettre de détecter un « mouvement objectif », un mouvement « absolu » ?
La seule chose que la relativité ancienne admettait comme « relatif », c’étaient les vitesses des déplacements des objets les uns par rapport aux autres, objets matériels mais aussi lumière. Cette « relativité », selon laquelle il n’y a pas de vitesse absolue pour des déplacements rectilignes uniformes, signifiait que les vitesses se comparaient, en s’additionnant ou se soustrayant suivant les cas…
Ensuite, est venue un autre principe qui, lui, est apparu absolu : la constance de la vitesse de la lumière, vitesse qui ne s’additionnait pas et ne se soustrayait pas, même si l’observateur se déplaçait par rapport au rayon lumineux (ou au photon lumineux).
D’où le paradoxe d’Einstein dans le cas extrême ou l’observateur se déplace à la même vitesse et dans la même direction que le rayon lumineux.
On se souvient que, paradoxalement, le principe de relativité énonce qu’il y aurait non un relatif mais deux absolus : les lois et la vitesse de la lumière. Ce sont deux absolus car ils sont inchangés en modifiant le système d’observation par un mouvement rectiligne uniforme ou en modifiant le mouvement de la source de lumière.
Mais ces deux principes de la relativité ont un défaut : ils s’opposent entre eux !!!
Quelle est la contradiction entre les deux principes de relativité qu’Einstein a réussi à combiner pour donner sa théorie de la relativité restreinte ? C’est premièrement le fait que les phénomènes sont les mêmes par rapport à deux repères en déplacement rectiligne et uniforme l’un par rapport à l’autre, et, deuxièmement, que la lumière a la même vitesse dans le vide dans toutes les situations et circonstances, quel que soit le mouvement de la source et celui de l’observateur. Comment Einstein a-t-il souligné la contradiction ? Par une expérience de pensée : un observateur se déplace uniformément en ligne droite en suivant un rayon lumineux. Le mouvement de l’observateur ne doit pas changer le phénomène qui est observé et donc il devrait observer un photon immobile selon un principe et il devrait observer un photon à la vitesse de la lumière selon le second principe !!! C’est assez dérangeant évidemment…
Et il a fallu toute l’ingéniosité d’Einstein pour démontrer que cette contradiction n’était pas diamétrale !
Où résidait l’erreur de formulation de la relativité ancienne, celle de la physique avant Einstein ? Eh bien, elle tenait dans la relativité des vitesses. Si un observateur se déplaçait par exemple dans la même direction qu’un objet observé, on pensait que la relativité s’exprimait par addition ou soustraction des vitesses, suivant que les deux mouvements (celui de l’observateur et celui de l’observé) étaient dans le même sens ou dans le sens contraire. Ce qui faisait que, dans l’exemple d’un observateur se déplaçant à la même vitesse, on soustrayait et on trouvait une vitesse nulle.
Einstein devait montrer que, même pour des déplacements rectilignes à vitesse constante, il n’y avait pas une simple addition ou soustraction. Cela devait être remplacé par une formule comprenant la vitesse de la lumière et qui signifiait justement que l’on n’additionnait rien à la vitesse de la lumière et que la lumière ne changeait jamais de vitesse, même si elle était vue par un observateur en mouvement : c’était en fait une formule non-linéaire contenant une racine de la quantité (1-v²/c²).
L’idée que les vitesses ne s’additionnaient pas ou ne se soustrayaient pas n’était déjà pas évidente mais on verra, avec la relativité restreinte puis généralisée (pour intégrer la gravitation) que la physique était contrainte non à une réforme mais à une véritable révolution !!! L’écoulement régulier du temps mais aussi la notion de simultanéité d’événements étaient ainsi renversé, ainsi que la constance d’une longueur ou d’une masse en mouvement !!! Devaient encore s’y rajouter découverte, vérifiée ensuite par l’expérience, d’une inertie de l’énergie (y compris celle du rayonnement) !!!
Einstein, lui-même expliquait :
« C’est au cours de cette année passée à Aarau que me vint à l’esprit la question suivante : si l’on poursuit une onde lumineuse à la vitesse de la lumière, on se trouve face à un champ d’ondes indépendant du temps (c’est-à-dire stationnaire). Mais il n’existe, semble-t-il, rien de tel. C’est ainsi que je fis tout jeune, la première expérience de pensée concernant la théorie de la relativité restreinte. » (Einstein dans « Esquisse biographique »)
« Dès les années 1900, c’est-à-dire peu après le travail de pionnier de Planck, des considérations de cet ordre me montrèrent clairement que ni la mécanique ni la thermodynamique ne pouvaient prétendre (sauf dans des cas limites) à une validité exacte. je désespérais peu à peu de la possibilité de découvrir les vraies lois en appuyant mes efforts de construction sur des faits connus… Mais comment trouver un principe général du même type que celui de la thermodynamique ? Au bout de dix ans de réflexion, ce principe émergea d’un paradoxe auquel je m’étais déjà heurté à l’âge de seize ans. Si je poursuis un rayon lumineux à la vitesse c (vitesse de la lumière dans le vide), je devrais percevoir ce rayon de lumière comme un champ électromagnétique oscillant sur place dans l’espace ; or, il semble bien qu’il n’existe rien de tel ni dans le domaine de l’expérience, ni selon les équations de Maxwell. Dès le début, il me parut intuitivement clair que, du point de vue d’un tel observateur, tout devait se passer selon les mêmes lois que pour un observateur immobile par rapport à la Terre. Car comment le premier observateur pourrait-il être en mesure de savoir, ou de constater, qu’il est dans un état de mouvement uniforme rapide ? On voit que ce paradoxe contient déjà en germe la théorie de la relativité restreinte. Bien sûr, chacun sait aujourd’hui que toutes les tentatives pour élucider ce paradoxe de manière satisfaisante étaient vouées à l’échec tant que l’axiome posant le caractère absolu du temps, ou de la simultanéité, restait subrepticement ancré dans notre inconscient. Reconnaître clairement cet axiome et son caractère arbitraire, c’est déjà trouver la solution du problème…
L’existence de principe de règles, et celles d’horloges (idéales ou parfaites) ne sont pas des hypothèses indépendantes l’une de l’autre. Car un signal lumineux réfléchi dans un mouvement de va-et-vient entre les extrémités d’une règle rigide représente une horloge idéale, à condition de supposer que la constance de la vitesse de la lumière dans le vide ne conduit à aucune contradiction.
Le paradoxe exposé ci-dessus peut dès lors être formulé ainsi : selon les règles utilisées en physique classique pour convertir les coordonnées spatiales et le temps d’un événement, lorsque l’on passe d’un système inertiel à un autre, sont incompatibles (bien que chacune de ces hypothèses, prises isolément, soit confirmée par l’expérience) :
1) constance de la vitesse de la lumière (dans un système inertiel, ce qui signifie l’indépendance par rapport à la vitesse de la source et à la direction de propagation)
2) indépendance des lois (et donc aussi de la loi de constance de la vitesse de la lumière) par rapport aux choix du système inertiel (principe de relativité restreinte).
L’idée sur laquelle repose la théorie de la relativité restreinte est la suivante : les hypothèses 1) et 2) sont incompatibles entre elles si, pour le changement des coordonnées et des temps relatifs à des événements, on se fonde sur des relations d’un type nouveau (les « transformations de Lorentz »)…
Le principe général de la théorie de la relativité restreinte est contenu dans le postulat suivant : les lois de la physique sont invariantes par les transformations de Lorentz (lors du passage d’un système inertiel à n’importe à n’importe quel autre système inertiel)…
Nous allons maintenant nous demander quelles sont les connaissances ayant un caractère définitif que la physique doit à la théorie de la relativité restreinte.
1) Il n’y a pas de simultanéité pour des événements distants ; il n’y a donc pas non plus d’action à distance immédiate, au sens de la mécanique newtonienne. Si l’introduction d’actions à distance se propageant à la vitesse de la lumière reste concevable dans le cadre de cette théorie (la relativité restreinte), elle apparaît néanmoins comme fort peu naturelle ; il est en effet impossible, dans une telle théorie, de trouver une formulation raisonnable du principe de conservation de l’énergie. La réalité physique semble donc devoir être, inévitablement, décrite au moyen de fonctions continues de l’espace. De ce fait, le point matériel ne devrait plus être considéré comme un concept fondamental de la théorie.
2) Les principes de conservation de l’impulsion et de conservation de l’énergie se fondent en un seul et même principe. La masse inerte d’un système fermé est identique à son énergie, de sorte que la masse est éliminée en tant que concept autonome…
La théorie de la relativité restreinte est redevable de son existence aux équations de Maxwell. A l’inverse, c’est seulement à l’aide de la théorie de la relativité restreinte que l’on peut, d’un point de vue formel, comprendre ces dernières de manière satisfaisante. Les équations de Maxwell sont les équations du champ, invariantes par transformation de Lorentz… » (Einstein dans « Eléments autobiographiques »)
« On sait fort bien, depuis l’Antiquité grecque, que lorsqu’on décrit le mouvement d’un corps, on a besoin d’un deuxième corps servant de référence pour le mouvement du premier. Le mouvement d’une voiture est rapporté au sol, celui d’une planète à la totalité des étoiles fixes visibles. En physique, le corps qui sert de référence spatiale aux phénomènes est appelé « système de coordonnées ». On ne peut formuler les lois de la mécanique de Galilée et de Newton par exemple qu’en se servant d’un système de coordonnées.
Mais il ne faut pas choisir l’état de mouvement du système de coordonnées arbitrairement si l’on veut que les lois de la mécanique soient valables (il ne doit y avoir ni rotation, ni accélération). Un système de coordonnées autorisé par la mécanique est appelé « système inertiel ». Néanmoins, l’état de mouvement d’un tel système n’est pas déterminé de façon univoque par la nature. On appliquera au contraire l’axiome suivant : un système de coordonnées qui se meut en ligne droite et uniformément par rapport à un système inertiel est, lui aussi, un système inertiel. On entend dès lors par « principe de relativité restreinte » la généralisation de cette proposition, étendue à tout processus naturel quel qu’il soit : toute loi naturelle universelle, valable par rapport à un système de coordonnées K, doit être valable de la même façon, sans modification aucune, par rapport à un système de coordonnées K’ soumis à un mouvement de translation uniforme par rapport à K.
Le deuxième principe qui fonde la relativité restreinte est le « principe de la constance de la vitesse de la lumière dans le vide ». Cela signifie que la lumière a toujours, dans le vide, une vitesse de propagation déterminée, indépendamment de l’état de mouvement et de la source de lumière. Le physicien fait confiance à cet axiome en raison des succès de l’électrodynamique de Maxwell et Lorentz.
L’expérience corrobore remarquablement les deux principes cités ; pourtant, il semble impossible de les concilier logiquement. C’est finalement grâce à une modification de la cinématique, c’est-à-dire de la science des lois concernant l’espace et le temps du point de vue de la physique, que la relativité restreinte est parvenue à les accorder logiquement. Il s’est avéré que parler de simultanéité de deux événements n’avait de sens que par rapport à un système de coordonnées et que la forme d’un instrument de mesure ainsi que le rythme d’une horloge devaient dépendre de leur état de mouvement par rapport au système de coordonnées. » (Einstein dans « Qu’est-ce que la théorie de la relativité »)
Dumontais, répondant en lieu et place d’Einstein :
« Si je voyage à la vitesse de la lumière, est-ce que je me verrais dans un miroir placé en face de moi ? La question est légitime parce que :
– La lumière de mon visage se propage vers le miroir.
– Mais le miroir se déplace lui aussi à la vitesse de la lumière.
Conséquence : la lumière ne rattrapera jamais le miroir et je ne verrai pas mon visage.
MAIS :
– Si mon image disparaît au moment où je voyage à la vitesse de la lumière, à ce moment-là, juste à regarder le miroir, je saurais que je voyage à la vitesse de la lumière, et cela serait CONTRAIRE au principe de relativité. Tout mouvement rectiligne uniforme est relatif.
Conséquence : je vois mon image normalement, même à la vitesse de la lumière. Pourtant, pour que cela se produise, il faudrait que mon image aille plus vite que la lumière, afin de rattraper le miroir.
D’où la théorie de la relativité : la vitesse de la lumière est constante, autant pour moi que pour l’observateur qui me regarde depuis le quai d’une gare. Donc, c’est la distance et le temps qui sont relatifs. Avec la vitesse, le temps se dilate et les longueurs se contractent.
Tout cela basé sur les principes suivants :
– Aucune interaction n’est instantanée
– Il y a une vitesse maximum possible et c’est la vitesse de la lumière
– La vitesse de la lumière est la même pour tous les observateurs
– L’espace et le temps sont relatifs
J’espère vous avoir éclairé sur ces points, et si vous ne comprenez pas, ne vous en faites pas trop, vous n’êtes pas le seul. Je n’ai mentionné aucune équation, afin de ne pas vous embrouiller davantage, mais elles existent bel et bien, et ne sont pas trop difficiles d’accès. »
Albert Einstein, par la voix de Dumontais
Lee Smolin écrit :
« La relativité restreinte d’Einstein est fondée sur deux postulats : le premier est la relativité du mouvement et le second la constance et la relativité de la vitesse de la lumière. (…) Albert Einstein a sans doute été le physicien le plus important du 20ème siècle. Sa plus grande réussite est sans doute la découverte de la relativité générale, à ce jour notre meilleure théorie de l’espace, du temps, du mouvement et de la gravitation. Sa profonde perspicacité nous a appris que la gravité et le mouvement sont dans une intime relation, non seulement entre eux mais également avec la géométrie de l’espace et du temps. (…) Selon la théorie générale de la relativité d’Einstein, l’espace et le temps ne constituent plus un fond fixe et absolu. L’espace est aussi dynamique que la matière : il bouge et il change de forme. (…) Quelques siècles avant Einstein, Galilée avait découvert l’unification du repos avec le mouvement uniforme (en ligne droite à vitesse constante). A partir de 1907 environ, Einstein a commencé à s’interroger sur les autres types de mouvement, tel le mouvement accéléré. Dans le mouvement accéléré, la direction ou la vitesse varient. (…) C’est à ce moment qu’Einstein a fait l’avancée la plus extraordinaire. Il a réalisé que l’on ne pouvait pas distinguer les effets de l’accélération des effets de la gravité. (…) Dans une cabine d’ascenseur en chute libre, les passagers de la cabine ne sentiraient plus leur poids. (…) L’accélération de l’ascenseur en chute libre compense totalement l’effet de la gravité. (…) L’unification de l’accélération et de la gravitation a eu des conséquences importantes et, avant même que ses implications conceptuelles ne soient comprises, d’importantes implications expérimentales furent dégagées. Quelques prédictions en découlaient (…) par exemple que les horloges doivent ralentir dans un champ gravitationnel. (…) Ou encore que la lumière se courbe lorsqu’elle circule au travers d’un champ gravitationnel. (…) La théorie d’Einstein a des conséquences très importantes, puisque les rayons de lumière sont courbés par le champ gravitationnel qui, à son tour, réagit à la présence de la matière. La seule conclusion possible est que la présence de matière influence la géométrie de l’espace. (…) Si deux rayons de lumière sont initialement parallèles, ils peuvent se rencontrer, s’ils passent tous les deux près d’une étoile. Ils sont recourbés l’un vers l’autre. Par conséquent, la géométrie euclidienne (où les droites parallèles ne se rencontrent jamais) n’est pas adaptée au monde réel. De plus, la géométrie varie sans cesse, parce que la matière est sans arrêt en mouvement. La géométrie de l’espace n’est pas plate comme un plan infini. Elle est plutôt comme la surface de l’océan : incroyablement dynamique, avec de grandes vagues et de toutes petites rides. Ainsi, la géométrie de l’espace s’est révélée n’être qu’un autre champ. (…) Dans la relativité restreinte, l’espace et le temps forment, ensemble, une entité quadridimensionnelle qu’on appelle espace-temps. (…) L’unification einsteinienne du champ gravitationnel avec la géométrie de l’espace-temps était le signal de la transformation profonde de notre façon de concevoir la nature. Avant Einstein, l’espace et le temps avaient été pensés comme possédant des caractéristiques fixes, données une fois pour toutes : la géométrie de l’espace est, a été et sera toujours celle décrite par Euclide et le temps avance indépendamment de tout le reste. Les choses pouvaient se déplacer dans l’espace et évoluer dans le temps, mais l’espace et le temps eux-mêmes ne changeaient jamais. (…) La théorie générale de la relativité d’Einstein diffère complètement. Il n’y a plus de fond fixe. La géométrie de l’espace et du temps varie et évolue en permanence, ainsi que le reste de la nature. (…) Il n’y a plus un champ qui se déplace sur un fond géométrique fixe. Au contraire, nous avons une collection de champs, qui interagissent tous, les uns avec les autres, qui sont dynamiques, qui tous exercent une influence sur les autres, et la géométrie de l’espace-temps en fait partie. (…) La relativité générale a vite mené aux prédictions de phénomènes nouveaux, tels que l’expansion de l’univers, le Big Bang, les ondes gravitationnelles et les trous noirs, dont il existe, pour tous, de solides preuves expérimentales. (…) La leçon principale de la relativité générale était qu’il n’y avait pas de géométrie fixe du fond spatio-temporel. (…) Cela signifie que les lois de la nature doivent s’exprimer sous une forme qui ne présuppose pas que l’espace ait une géométrie fixe. C’est le cœur de la leçon einsteinienne. Cette forme se traduit en principe, celui d’indépendance par rapport au fond. Ce principe énonce que les lois de la nature peuvent être décrites dans leur totalité sans présupposer la géométrie de l’espace. (…) L’espace et le temps émergent de ces lois plutôt que de faire partie de la scène où se joue le spectacle. Un autre aspect de l’indépendance par rapport au fond est qu’il n’existe pas de temps privilégié. La relativité générale décrit l’histoire du monde au niveau fondamental en termes d’événements et de relations entre eux. Les relations les plus importantes concernent la causalité : un événement peut se trouver dans la chaîne causale qui mène à un autre événement. (…) Ce sont lesdits événements qui constituent l’espace. (…) Toute définition concrète de l’espace dépend du temps. Il existe autant de définitions de l’espace que de temporalités différentes. (…) La question fondamentale pour la théorie quantique de la gravitation est, par conséquent, celle-ci : peut-on étendre à la théorie quantique le principe selon lequel l’espace n’a pas de géométrie fixe ? C’est-à-dire peut-on faire une théorie quantique indépendante du fond, au moins en ce qui concerne la géométrie de l’espace ? (…) En 1916, Einstein avait déjà compris qu’il existait des ondes gravitationnelles et qu’elles portaient une énergie. Il a tout de suite remarqué que la condition de cohérence avec la physique atomique demande que l’énergie portée par les ondes gravitationnelles soit décrite en termes de la théorie quantique (dans « Approximate integration of the field of gravitation ». (…) Heisenberg et Pauli croyaient que, lorsqu’elles sont très faibles, on pouvait considérer les ondes gravitationnelles comme de minuscules ondulations qui viennent déranger une géométrie fixe. Si l’on jette une pierre dans un lac par un matin calme, elle provoquera de petites ondulations qui ne dérangeront que très peu la surface plane de l’eau, il sera alors facile de penser que les rides se déplacent sur un fond fixe donné par une surface. Mais quand les vagues sont fortes et turbulentes près d’une plage lors d’une tempête, cela n’a aucun sens de les considérer comme des perturbations de quelque chose de fixe. La relativité générale prédit qu’il existe des régions de l’univers où la géométrie de l’espace-temps évolue de façon turbulente comme les vagues qui viennent frapper la plage. Pourtant, Heisenberg et Pauli croyaient qu’il serait plus facile d’étudier d’abord les cas où les ondes gravitationnelles sont extrêmement faibles et peuvent être considérées comme de petites rides sur un fond fixe. Cela leur permettait d’appliquer les mêmes méthodes que celles qu’ils avaient développées pour l’étude des champs quantiques électromagnétiques qui se déplaceraient sur un fond spatio-temporel fixe. (…) Le résultat était que chaque onde gravitationnelle devait être analysée selon la méthode dictée par la mécanique quantique, comme une particule qu’on appelle graviton – analogue au photon, qui, lui, est un quantum du champ électromagnétique. Or, à l’étape suivante, un énorme problème s’est posé, car les ondes gravitationnelles interagissent entre elles. Elles interagissent avec tout ce qui a une énergie ; et elles-mêmes ont aussi une énergie. Ce problème n’apparaît pour les ondes électromagnétiques, puisque les photons interagissent avec les charges électriques et magnétiques, ils ne sont pas eux-mêmes chargés et, par conséquent, ils peuvent facilement traverser les autres photons. (…) Puisque les ondes gravitationnelles interagissent les unes avec les autres, elles ne peuvent plus être pensées comme se déplaçant sur un fond fixe. Elles modifient le fond sur lequel elles se déplacent. (…) Il ne suffit pas d’avoir une théorie des gravitons fabriqués à partir de cordes se tortillant dans l’espace (théorie des cordes). Nous avons besoin d’une théorie de ce qui fait l’espace, c’est-à-dire une théorie indépendante du fond. (…) Les approches les plus réussies, à ce jour, de la gravité quantique utilisent la combinaison de trois idées fondamentales : que l’espace est émergent, que la description est fondamentalement discrète et que cette description fait intervenir la causalité de façon cruciale. »
Sur la philosophie de la Relativité d’Einstein, l’exposé de Feynman dans son Cours de Physique :
« Le principe de la relativité fut d’abord énoncé par Newton dans l’un de ses corollaires aux lois du mouvement :
« Les mouvements de corps placés dans un certain espace sont les mêmes les uns par rapport aux autres, que cet espace soit au repos ou qu’il avance uniformément selon une ligne droite. »
Ceci signifie, par exemple, que si un vaisseau spatial se déplace à une vitesse uniforme, toutes les expériences réalisées et tous les phénomènes dans le vaisseau spatial paraîtront identiques à ce que l’on obtiendrait si le vaisseau ne se déplaçait pas, pourvu, bien sûr, que l’on ne regarde pas à l’extérieur.
C’est là la signification du principe de la relativité. C’est une idée simple, et la seule question est de savoir s’il est vrai que dans toutes les expériences réalisées à l’intérieur d’un système en mouvement, les lois de la physique paraissent les mêmes que si le système était resté au repos…
Si nous effectuons une transformation des coordonnées (correspondant à un mouvement relatif rectiligne et uniforme) dans les lois de Newton, nous trouverons que ces lois se transforment en des lois identiques, c’est-à-dire que les lois de Newton ont la même forme dans un système en mouvement que dans un système stationnaire, et de ce fait il est impossible en réalisant des expériences mécaniques, de dire si le système est ou non en mouvement.
Le principe de relativité a été pendant longtemps utilisé en mécanique. Il fut utilisé par diverses personnes, en particulier par Huygens, pour obtenir les lois des collisions des boules de billard, d’une manière très semblable de celle pour discuter la conservation de la quantité de mouvement.
Au siècle passé, l’intérêt pour ce principe augmenta à la suite des recherches concernant les phénomènes de l’électricité, du magnétisme et de la lumière.
Une longue suite d’études soigneuses de ces phénomènes par de nombreuses personnes aboutit aux équations de Maxwell du champ électromagnétique, qui réunissent dans un système uniforme l’électricité, le magnétisme et la lumière.
Cependant les équations de Maxwell ne semblent pas obéir au principe de la relativité. C’est-à-dire, si nous transformons les équations de Maxwell par la substitution des nouvelles coordonnées (dues à un déplacement relatif rectiligne et uniforme), leurs formes ne restent pas les mêmes ; de ce fait, les phénomènes électriques et optiques dans un vaisseau spatial en mouvement devraient être différents de ceux dans un vaisseau au repos.
Ainsi pourrait-on utiliser ces phénomènes optiques pour déterminer la vitesse du vaisseau ; en particulier, on pourrait déterminer la vitesse absolue du vaisseau ; en particulier on pourrait déterminer la vitesse absolue du vaisseau en faisant des mesures optiques ou électriques adéquates.
Une des conséquences des équations de Maxwell est que s’il y a une perturbation dans le champ telle que de la lumière soit créée, ces ondes électromagnétiques s’éloignent dans toutes les directions de la même manière et à la même vitesse c, ou 300.000 km/sec.
Une autre conséquence des équations est que, si la source de la perturbation se déplace, la lumière émise parcourt l’espace à la même vitesse c.
Ceci est analogue au cas du son, la vitesse des ondes sonores étant de la même manière indépendante du mouvement de la source.
Cette indépendance du mouvement de la source, dans le cas de la lumière, fait naître un très intéressant problème :
Supposons que nous soyons dans une voiture qui roule à une vitesse v, et que la lumière venant de l’arrière passe à côté du véhicule avec la vitesse c…
Ce qui signifie que, selon la transformation de Galilée, la vitesse apparente de la lumière qui passe, mesurée dans la voiture, ne doit pas être c mais doit être c-v…
Un certain nombre d’expériences basées sur cette idée générale furent tentées pour déterminer la vitesse de la terre, mais ce furent chaque fois des échecs – elles ne donnaient aucune vitesse.
Nous allons discuter une de ces expériences en détail, pour montrer exactement ce qui fut fait et quel était le problème ; il y avait un problème, bien sûr, quelque chose n’allait pas dans les équations de la physique. Qu’est-ce que cela pouvait-il bien être ?
Lorsque l’échec des équations de la physique dans les cas précédents fut mis en évidence, la première idée fut que la difficulté devait se trouver dans les nouvelles équations de Maxwell de l’électrodynamique, qui n’avaient que vingt ans d’âge à cette époque. Il semblait presque évident que ces équations devaient être fausses, aussi la chose à faire était de les modifier d’une manière telle qu’avec la transformation Galiléenne le principe de la relativité soit satisfait. Lorsque ceci fut essayé, les nouveaux termes qu’on devait introduire dans les équations conduisirent à des prédictions de nouveaux phénomènes électriques dont l’existence fut infirmée par l’expérience, aussi cette tentative dut être abandonnée.
Alors il devint petite à petit manifeste que les lois de Maxwell de l’électromagnétisme étaient correctes, et qu’il fallait rechercher ailleurs la difficulté.
Pendant ce temps, H. A. Lorentz remarquait une chose curieuse : les équations de Maxwell conservaient la même forme quand une transformation non-linéaire de la coordonnée d’espace et de celle de temps, en divisant par la racine carrée de la quantité (1-v²/c²) où v était la vitesse de déplacement du repère et c la vitesse de la lumière, était appliquée. Cette transformation des coordonnées est appelée « transformation de Lorentz ».
Einstein, suivant une suggestion initialement avancée par Poincaré, proposa alors que « toutes les lois physiques doivent être telles qu’elles restent inchangées dans une transformation de Lorentz ».
En d’autres termes, nous devons changer non les lois de l’électromagnétisme, mais les lois de la mécanique.
Comment devons-nous modifier les lois de Newton de telle sorte qu’elles restent inchangées dans la transformation de Lorentz ?
Si nous nous fixons ce but, nous devons réécrire les équations de Newton avec la seule obligation que la masse soit divisée par la racine de la quantité (1-v²/c²). Lorsque ce changement est réalisé, les lois de Newton et les lois de l’électromagnétisme sont en accord.
Si ensuite nous utilisons la transformation de Lorentz en comparant les mesures de Durand avec celles de Dupont, nous ne seront jamais capables de détecter si l’un ou l’autre se déplace, parce que la forme de toutes les équations sera la même dans les deux systèmes de coordonnées…
Nous allons poursuivre la discussion du principe de relativité d’Einstein et de Poincaré, sous l’aspect de son influence sur nos idées en physique et sur les autres branches de la pensée humaine.
Poincaré énonça le principe de la relativité de la manière suivante :
« Selon le principe de la relativité, les lois des phénomènes physiques doivent être les mêmes pour un observateur fixe et pour un observateur en mouvement de translation uniforme relativement au premier, de telle sorte que nous n’ayons pas, ou que nous ne puissions avoir aucun moyen de discerner si oui ou non nous suivons un tel mouvement. »
Lorsque cette idée se propagea à travers le monde, elle causa un grand émoi parmi les philosophes, particulièrement chez les « philosophes de salon » qui vont disant « Oh, c’est très simple : la théorie d’Einstein dit que tout est relatif ! »
En fait, un nombre étonnamment grand de philosophes, et pas seulement ceux que l’on rencontre dans les salons (mais plutôt que de les embarrasser, nous les appellerons simplement des philosophes de salon) disent : « Einstein a dit que tout est relatif, et ceci a eu une influence profonde sur nos idées. »
De plus, ils disent : « On a démontré en physique que les phénomènes dépendent de notre système de référence. » Nous avons entendu cela bien souvent, mais il est difficile de voir ce que cela signifie. Il est probable que les systèmes de références auxquels on se réfère étaient initialement les systèmes de coordonnées que nous utilisons dans l’analyse de la théorie de la relativité.
Ainsi on considère que le fait que « les choses dépendent de votre système de référence » a eu un profond effet sur la pensée moderne. On peut bien se demander pourquoi, car, après tout, que les choses dépendent du point de vue de chacun est une idée si simple qu’il n’était pas nécessaire d’être passé par toutes les difficultés de la théorie physique de la relativité pour pouvoir la découvrir.
Que ce que l’on voit dépende de son système de référence est certainement connu de tout un chacun qui se promène, car il voit un piéton s’approchant d’abord de face et ensuite de dos ; il n’y a rien de plus profond dans la plupart des philosophies qui se réclament de la théorie de la relativité que la remarque qu’« Une personne paraît différente de face et de dos. » La vieille histoire d’un éléphant que plusieurs aveugles décrivent d’une manière différente est peut-être un autre exemple de la théorie de la relativité du point de vue des philosophes.
Mais il doit y avoir certainement des choses plus profondes dans la théorie de la relativité que cette simple remarque qu’ « Une personne semble différente vue de face et vue de dos. » La relativité est plus profonde que cela, car nous ne pouvons faire à partir d’elle des prédictions définies. Cela serait évidemment plutôt remarquable de pouvoir prédire le comportement de la nature à partir d’une seule observation aussi simple.
Une autre école de philosophie s’est trouvée très mal à l’aise avec la théorie de la relativité, lorsqu’elle affirme que nous ne pouvons pas déterminer notre vitesse absolue sans regarder quelque chose à l’extérieur ; ils disent : « Il est évident qu’on ne peut mesurer sa vitesse sans regarder à l’extérieur. Il va de soi que parler de la vitesse d’une chose sans regarder à l’extérieur n’a pas de signification ; les physiciens sont stupides d’avoir pensé différemment, mais ils réalisent maintenant qu’ils étaient dans l’erreur. Si seulement nous les philosophes, nous nous étions rendu compte des problèmes des physiciens, nous aurions pu affirmer immédiatement, par une simple réflexion, qu’il est impossible de dire à quelle vitesse quelqu’un se déplace sans regarder à l’extérieur, et nous aurions pu apporter une énorme contribution à la physique. »
Ces philosophes sont toujours parmi nous, se débattant à la périphérie pour essayer de nous dire quelque chose, mais ils ne comprennent jamais vraiment les subtilités et les profondeurs du problème.
Notre aptitude à détecter le mouvement absolu est un résultat de l’expérience et non un résultat de la pure réflexion, comme nous pouvons facilement le montrer. Au début, Newton croyait que, s’il se déplaçait avec une vitesse uniforme selon une ligne droite, personne ne pourrait dire à quelle vitesse il allait. En fait Newton, le premier, énonça le principe de relativité, et nous l’avons cité au chapitre précédent. Pourquoi alors les philosophes n’ont-ils pas fait, à l’époque de Newton, tout ce foin à propos du fameux « tout est relatif » et ainsi de suite ? Parce que ce ne fut pas avant le développement de la théorie de Maxwell de l’électrodynamique que furent découvertes les lois de physique suggérant qu’on pourrait mesurer sa vitesse sans regarder à l’extérieur ; on découvrit rapidement PAR L’EXPERIENCE (souligné par l’auteur) que ce n’était pas possible.
Est-il absolument, définitivement, philosophiquement nécessaire que l’on ne puisse être capable de dire à quelle vitesse on se déplace sans regarder à l’extérieur ? Une des conséquences de la relativité fut le développement d’une philosophie qui disait :
« Vous ne pouvez définir que ce vous pouvez mesurer ! Puisqu’il va de soi que l’on ne peut mesurer une vitesse sans voir par rapport à quoi on la mesure, il est alors clair que la vitesse absolue n’a aucune « signification ». Les physiciens auraient dû réaliser qu’ils ne peuvent parler que de ce qu’ils peuvent mesurer. »
Mais tout le problème est là : que nous puissions ou non définir une vitesse absolue est la même chose que le problème de savoir si oui ou non nous pouvons détecter par une expérience, sans regarder au dehors, si nous nous déplaçons.
En d’autres termes, qu’une chose soit mesurable ou non ne peut se décider a priori par la seule pensée, cela ne relève que de l’expérience. Etant donné le fait que la vitesse de la lumière vaut 300.000 kilomètres par seconde, on trouvera peu de philosophes qui affirmeront calmement qu’il va de soi que, si la lumière va à 300.000 kilomètres par seconde à l’intérieur d’une voiture et que la voiture se déplace à 150.000 kilomètres par seconde, la lumière se déplacera également à 300.000 kilomètres par seconde par rapport à un observateur au sol. C’est un fait choquant pour eux ; ceux qui affirment que c’est évident, trouvent lorsque vous leur proposez un fait précis, que ce n’est plus si évident.
Finalement, il y a même une philosophie affirmant qu’on ne peut détecter aucun mouvement sans regarder à l’extérieur.
C’est simplement faux en physique. Il est vrai qu’on ne peut pas percevoir un mouvement « uniforme en ligne droite », mais si toute la pièce tournait nous le saurions certainement, car tout le monde serait projeté contre le mur – il y aurait toutes sortes d’effets « centrifuges ». Que la terre tourne autour de son axe peut être déterminé sans regarder les étoiles, par l’intermédiaire du pendule de Foucault par exemple.
Il n’est donc pas vrai que « tout est relatif » ; ce n’est que la « vitesse uniforme » qui est indécelable, si l’on ne regarde pas à l’extérieur. Une rotation uniforme autour d’un axe fixe peut être détectée. Lorsqu’on raconte ceci à un philosophe, il est très fâché de ne pas avoir pu réellement comprendre cela, car il lui semble impossible que l’on soit capable de déterminer la rotation autour d’un axe sans regarder à l’extérieur.
Si le philosophe est assez valable, il peut revenir après un peu de temps et dire :
« Je comprends. Nous n’avons pas en réalité de chose telle qu’une rotation absolue ; nous sommes en réalité en train de tourner relativement aux étoiles, voyez-vous. Et ainsi une certaine influence exercée par les étoiles sur l’objet doit créer une force centrifuge. »
Pour autant que nous sachions, ceci est vrai ; nous n’avons aucune manière à l’heure actuelle de dire s’il y aurait des forces centrifuges en l’absence des étoiles et des nébuleuses tout autour. Nous n’avons pas encore été en mesure de faire l’expérience d’écarter toutes les nébuleuses et de mesurer notre rotation, ce qui fait que tout simplement nous ne savons pas.
Nous devons admettre que le philosophe peut être dans le vrai. Il revient donc tout à fait satisfait et dit :
« Il est absolument nécessaire que le monde en définitive soit ainsi : la rotation « absolue » ne signifie rien ; elle s’effectue simplement par rapport aux nébuleuses. »
Alors nous lui répondons :
« Maintenant, mon ami, est-il ou n’est-il pas évident qu’une vitesse uniforme en ligne droite, « relativement aux nébuleuses » doit ne produire aucun effet à l’intérieur de la voiture ? »
Maintenant que le mouvement n’est plus absolu, mais est un mouvement « relatif par rapport aux nébuleuses », cela devient une question mystérieuse, et une question à laquelle on ne peut répondre que par l’expérience.
Quelles sont alors les influences philosophiques de la théorie de la relativité ? Si nous nous limitons aux influences au sens de « quels genres de nouvelles idées et suggestions » sont apportés aux physiciens par le principe de la relativité, nous pourrions en décrire certains de la manière qui suit. La première découverte est, essentiellement, que même les idées qui ont été acceptées pendant un temps très long et qui ont été vérifiées très précisément peuvent être fausses. C’est une découverte choquante, bien sûr, que les lois de Newton soient fausses, après toutes les années où elles semblaient être précises. Il est clair, bien sûr, que ce n’étaient pas les expériences qui étaient fausses, mais qu’elles étaient réalisées simplement dans un domaine limité de vitesse, domaine si petit que les effets relativistes ne pouvaient être évidents. Mais néanmoins nous avons maintenant un point de vue beaucoup plus humble de nos lois physiques – tout peut être faux !
Deuxièmement, si nous avons un ensemble d’idées « étranges » telles que le temps ralentit lorsqu’on se déplace, etc., le fait que de « les prendre en sympathie ou non » est une question sans objet. La seule question qui ait un sens est de savoir si les idées sont en accord avec ce qu’on trouve expérimentalement. En d’autres termes, les « idées étranges » doivent simplement être en accord avec l’expérience, et la seule raison que nous ayons de discuter le comportement des horloges, etc., est de démontrer que bien que la notion de dilatation du temps soit étrange, elle est en accord avec la manière dont nous mesurons le temps.
Enfin, il y a une troisième suggestion un peu plus technique mais qui s’est révélée être d’une très grande utilité dans notre étude des autres lois physiques, c’est de « regarder la symétrie des lois » ou, plus précisément, de regarder la manière dont les lois peuvent être transformées tout en gardant une forme invariante. Lorsque nous avons étudié la théorie des vecteurs, nous avons remarqué que les lois fondamentales du mouvement ne sont pas changées lorsque nous tournons le système de coordonnées, et maintenant nous apprenons qu’elles ne sont pas changées lorsque nous modifions les variables d’espace et de temps d’une manière particulière, donnée par la transformation de Lorentz. Ainsi, cette idée d’étudier les structures et les opérations pour lesquelles les lois fondamentales ne sont pas modifiées, est apparue très utile. »
Nous avons discuté longuement de la relativité restreinte, la première forme de loi de relativité d’Einstein. Venons-en à la deuxième : la relativité généralisée.
Voici comment Einstein expose le passage de la relativité restreinte à la relativité généralisée dans « Documents autobiographiques » :
« C’est en travaillant à Berne que je réfléchis à la théorie de la relativité. La relativité restreinte avait déjà quelques années. Le principe de relativité était-il limité aux systèmes inertiels, c’est-à-dire aux systèmes de coordonnées qui ont, les uns par rapport aux autres, un mouvement uniforme (transformations linéaires des coordonnées) ? Mon sens intuitif du formalisme me disait qu’il n’en était vraisemblablement rien. Pourtant, le principe d’inertie sur lequel reposait toute la mécanique développée jusqu’alors semblait exclure tout élargissement du principe de relativité. En effet, si l’on introduit un système de coordonnées en mouvement accéléré (accéléré par rapport au système inertiel), par rapport à ce système accéléré, une masse ponctuelle « isolée » ne se déplace plus en ligne droite à une vitesse uniforme. Un esprit libre que des habitudes intellectuelles n’auraient pas inhibé se serait alors demandé : ce comportement me donne-t-il les moyens de distinguer un système inertiel d’un système qui ne l’est pas ? Il serait alors forcément arrivé (du moins dans le cas d’une accélération linéaire uniforme) à la conclusion que tel n’est pas le cas. Car on peut très bien interpréter le comportement des corps par rapport à un système de coordonnées possédant ce type d’accélération comme étant dû à l’action d’un champ de gravitation. Interprétation rendue possible par le fait empirique que, dans un champ de gravitation, l’accélération d’un corps est, là aussi, toujours la même et indépendante de la nature du corps. Cette découverte (principe d’équivalence) rendait vraisemblable l’idée que les lois de la nature doivent être invariantes sous l’effet de transformations appartenant à un groupe plus large que celui des transformations de Lorentz (extension du principe de relativité) ; mais ce n’est pas tout : elle laissait aussi supposer que cette extension devait conduire à une théorie plus profonde du champ de gravitation. Je ne doutais pas le moins du monde que cette idée fût juste dans son principe. Mais les difficultés mathématiques de sa mise en œuvre me semblaient presque insurmontables. Des considérations élémentaires firent vite apparaître que le passage à un groupe de transformations plus large était incompatible avec l’interprétation physique directe des coordonnées d’espace et de temps qui m’avait conduit à la théorie de la relativité restreinte… L’analyse que H. Minkowski avait faite des bases formelles de la théorie de la relativité restreinte s’avéra extrêmement importante. Elle peut être résumée en une phrase : l’espace quadridimensionnel possède une métrique pseudo-euclidienne (invariante) ; celle-ci détermine les caractéristiques expérimentalement observables de la métrique de l’espace ainsi que la forme du principe d’inertie, et, au-delà, la forme des systèmes d’équations qui sont invariantes par transformation de Lorentz. Dans cet espace, il existe des systèmes de coordonnées privilégiés, à savoir les systèmes de coordonnées quasi-cartésiens qui sont en l’occurrence les seuls systèmes « naturels » (systèmes inertiels). »
Expérience de pensée d’Einstein
Qu’est-ce que la relativité d’Einstein ?
Pourquoi il n’y a pas de trajectoire du mouvement des particules en physique quantique ?
Que savons-nous sur la lumière ?
Des exemples concrets de la relativité restreinte




Messages
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 5 février 2019, 07:00, par JFP/Jean-François POULIQUEN.
Bonjour.
___L’ordre de points ou grains d’un nuage quantique, est d’autant pas une liste ordonnée de ses éléments, que des grains partent et d’autres viennent et considérés comme des remplacements, car des échanges se font entre grains de matière réelle et grains de matière virtuelle, par les grains et non par l’ensemble des grains. Donc quand un grain s’en va, la liste change, et quand il est remplacé la liste change encore. Il n’y a donc pas un ordre des grains du nuage à respecter, car cet ordre change constamment. Et bien pour vos articles du rel, il faut considérer que c’est un peu pareil, car à chaque création, l’ordre des articles peuvent changer, si l’article s’insère dans la liste et non en fin de liste. La liste des articles est donc une vraie liste non aléatoire, mais non maîtrisable.
Amicalement.
JFP/Jean-François POULIQUEN.
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 5 février 2019, 07:06, par Robert Paris
La matière, contrairement aux articles, est dans l’impossibilité d’interagir par contact !
Donc il lui faut des particules d’interaction !
2. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 5 février 2019, 10:29, par JFP/Jean-François POULIQUEN.
___Pourquoi affirmer que la matière ne peut pas interagir avec elle-même par contact ?? Y a t-il un articule qui démontre cette affirmation ou une loi ou autre ??
___Tout le problème quand on parle de matière, et bien on ne sait vraiment de quoi on parle, car cela reste trop vaste. Cette matière réelle ou virtuelle est composée d’éléments. Donc si l’ensemble ne peut pas être en contact et bien cela me semble faux en partie, car pour une partie des éléments constituant la matière cela peut être vrai. Les électrons externes par rapport au noyau de l’atome, sont plus ou moins en contact presque permanent avec des électrons d’autres noyaux, où il y a même des échanges d’électrons entre atomes. Ces contacts sont même des chocs, mais non des chocs entre électrons eux-mêmes mais des chocs entre les constituants des électrons que je considère comme des grains, et donc certains grains de ces électrons s’échangent entre le vide de l’espace quantique, mais aussi entre d’autres grains proche d’autres électrons d’autres noyaux proches. Pour vous les nuages formant les électrons se touchent presque, ou ils s’effleurent, se combinent par l’intermédiaire d’autres particules, s’échangent encore par des particules d’interaction, mais pour moi, ces particules d’interaction ne sont pas une nécessité, car déjà ils peut y avoir des échanges sans collision d’une part, et d’autre part on peut aussi avoir des échanges avec collisions et engendrant d’autres effets qui sont sans doutes des particules d’interaction, mais des particules résultant de chocs et non vraiment d’interaction comme des liens. Ces micro-chocs de grains d’électrons différents c’est en gros de l’énergie perdue, mais redonnée par l’énergie du vide. Et à ce propos la notion de "CHALEUR" est cette notion de chocs de grains d’électrons ou autre, car plus la matière est chaude, et plus les électrons internes au noyau changent de couche supérieure rentrant en collision avec les mêmes couches d’autres atomes proches, et ce sont ces collisions qui donnent cette notion de chaleur, et donc la matière est en contact avec elle-même. L’interaction est pour moi synonyme de chocs, et les effets peuvent être divers. Plus la matière est froide et moins elle interagit avec elle-même, mais plus elle est chaude et plus il y a de chocs et donc de contacts vec elle-même. C’est donc la quantité de chocs qui détermine la température, et on peut assimiler chocs comme contacts.
Amicalement.
JFP/Jean-François POULIQUEN.
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 5 février 2019, 11:26, par Robert Paris
« Pourquoi affirmer que la matière ne peut pas interagir avec elle-même par contact ?? Y a t-il un articule qui démontre cette affirmation ou une loi ou autre ?? » écris-tu !!!
Mais oui ! Il y a tout cela et d’abord l’observation d’un tel contact n’a jamais eu lieu. Ensuite, il y a des lois qui l’empêche et même plusieurs !!
Il y a l’écrantage de la charge qui augmente la répulsion plus les particules s’approchent.
Il y a le principe de Pauli qui empêche la matière de s’agglomérer.
Il a la "démographie" des fermions qui est anti-agglutination contrairement à la "démographie" bosonique qui est l’inverse.
Il y a de nombreuses forces de répulsion bien plus fortes que l’attraction gravitationnelle très faible à l’échelle des particules.
Il y a le fait qu’en des temps très courts, la propriété de masse saute à une autre particule et donc les deux particules dites réelles (portant la masse) ne peuvent pas s’attirer.
Et j’en passe des meilleurs plus compliqués comme la force de répulsion du vide entre deux particules de matière...
3. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 5 février 2019, 15:31, par JFP/Jean-François POULIQUEN.
RE Bonjour.
___Vous savez des lois on s’en passe quand on est révolutionnaire, sinon on avance pas. Je ne vais pas réécrire les lois de Napoléon, mais les dernières sûrement où on se passe de quanta pour dire que c’est le photon tout seul comme un grand qui peut générer des particules est assez curieux, et ce pour ne pas employer d’autres adjectifs.
___Je pense que vous grossissez et déformez mes propos, car entre anti-agglutination et le verbe interagir sont des notions différentes, car je n’essaie pas se compacter pas agglutination et donc ne pas rester coller, mais interagir par contact vont dans le même sens, car je n’ai jamais dit que la matière au sens large pouvait rester coller à une autre matière mais avoir des contacts sur une partie de ses éléments, sachant comme je l’explique que se sont des contacts par chocs et que forcément après ces chocs il n’est plus de contact. D’ailleurs j’ai parlé de chocs et d’échanges, et donc échange ne veut pas dire agglomérer mais justement repousser mais échanger quand même. Je me demande d’ailleurs si nos contacts ne sont pas des chocs, car à en voir vos réponses, les explications n’y sont pas vraiment, tant vous êtes empressé de répondre. Que le principe de Pauli empêche que la matière agglutine, et bien je n’ai pas dit le contraire, car ce que j’explique se sont des chocs et non des collages ou des agglutinations et des rassemblements de quoi que ce soit.
___C’est curieux de déformer à ce point mes propos, d’autant que vos réponses n’en sont pas vraiment, car si il y avait eu un article de ce Pauli exprimant cette impossibilité que la matière puisse s’agglomérer, et bien j’aurai lu, mais là rien de tel. Donc quelques fois vous êtes ouvert et quelques fois complètement fermé. Je me répète, mais j’ai dit qu’une partie de la matière au sens atome pouvait être en contact avec d’autres atomes, mais ces contacts ne définissent en rien une colle, car justement ce sont des chocs constants, et je dis bien que par ces chocs il y a des échanges, mais implicitement ces chocs ne sont pas de la colle, sinon il n’y aurait plus de choc. Ce qui est fou, c’est que je décortique mes phrases en les allongeant pour qu’il n’y ait pas de confusion, et vous les prenez dans le sens contraire. C’est à ne rien comprendre votre façon de lire, car sûrement vous vous buttez sur un mot ou trois, et après cela ne correspond plus à ce que j’ai expliqué. Mais je crois savoir votre mécontentement ou votre agacement qui est par cette phrase : : [Tout le problème quand on parle de matière, et bien on ne sait vraiment de quoi on parle, car cela reste trop vaste.]. Vous prenez la "MOUCHE" mon cher Paris, c’est du moins ce que je pense. Encore une expression idiote, mais c’est comme ça.
___Pour cette histoire de principe de Pauli, et bien je suis aller voir ce qui est dit : : Ce principe interdit d’avoir deux électrons dans le même état quantique pour un système donné. Comme un état est un ensemble d’attributs, et bien en gros Pauli interdit d’avoir deux électrons à la même position et ayant le reste des caractéristiques identiques. Cela détermine aussi le nombre d’électrons par couche dans l’atome et suivant la couche. Après cela se généralise avec les autres particules Voici ce qui est dit par ce Wikipédia, mais apparemment non par un retour sur une citation de ce Pauli et par vous : : [L’état quantique d’une particule est défini par des « nombres quantiques ». Le principe d’exclusion interdit à tout fermion appartenant à un système de fermions d’avoir exactement les mêmes nombres quantiques qu’un autre fermion du système.]. Et bien je pense que vous avez omis ce bout de phrase "appartenant à un système de fermions" comme aussi "autre fermion du système". Les chocs entre ces grains d’électrons sont dans des systèmes différents, car il faut comprendre que c’est le noyaux de l’atome et l’ensemble des électrons qui définit un système, et si il y a deux atomes, et bien cela fait deux systèmes, et rien n’empêche d’avoir des chocs de parties d’électron entre deux systèmes différents, et ce même si ces électrons ont des couches identiques et même des nombres quantiques presque identiques, car la restriction est fait pour le système et non pour d’autres systèmes, ce qui fait que deux systèmes peuvent peuvent très bien s’entrechoquer. Ce n’est pas drôle d’aller à la pêche quand vous êtes de mauvaise fois, car les mouches sans doute.
___Pour ces accélérateurs de particules, l’écrantage est justement supprimé car c’est le but de faire "courir" à des vitesses proche de la lumière des particules en sens inverse et de les faire collisionner. Et bien dans la nature cela est gratuit et ne demande pas de très grande énergie au niveau des atomes, car la vitesse de la lumière et peut être même plus grande, et le sens inverse y est aussi, mais il faut de la chance, mais pas tant que cela, et donc les collisions existent forcément. Maintenant on ne parle absolument pas d’électrons qui s’entrechoquent mais des parties d’eux-mêmes que sont les grains pour moi, et pour vous des nuages. D’ailleurs dans cette image de deux électrons nuageux entrechoquons c’est très choquant, car cette notion de nuage n’a pas de consistance, et on n’aboutit pas à des vrais chocs.
___Après avec votre dernière phrase qui est: : [Il a la "démographie" des fermions qui est anti-agglutination contrairement à la "démographie" bosonique qui est l’inverse.] et bien je ne comprends rien car je ne sais pas ce que vous voulez dire exactement car est-ce une loi, un principe, un constat ou autre.
___Je ne sais pas pourquoi vous me parler de gravitation à cette échelle. Au niveau des forces de répulsions et bien cela peut encore s’expliquer, mais on ne parle pas d’électron mais de ses constituants, et donc si l’union fait la force pour le simple électron, il faut que cette force soit moindre si elle est décomposée et divisée. De plus il y a un paradoxe, car dans certaines des citations comme les vôtres d’ailleurs un photon est porteur d’une particule positive et d’un autre de charge opposée, et le combat est le même que celui de la répulsion, car le photon doit aussi combattre l’attraction, car répulsion ou attraction, c’est identique au niveau des forces employées.
___[Il y a le fait qu’en des temps très courts, la propriété de masse saute à une autre particule et donc les deux particules dites réelles (portant la masse) ne peuvent pas s’attirer.] Cette phrase je ne la comprend pas car je ne sais pas de quelle particule dont on parle et qui saute d’une particule virtuelle à une autre, car de plus pour sauter d’un point à un autre il faut déjà être sur le point de départ qui est une particule mais laquelle.
___[Et j’en passe des meilleurs plus compliqués comme la force de répulsion du vide entre deux particules de matière..] Et bien ne passé pas M. Paris et donnez moi simplement les articles où je peux aller voir, ce dont vous voulez parler.
___Pour le redire encore, l’exclusion de Pauli est respectée, car deux grains de deux systèmes différents entrant en collision est possible, car rien que les directions opposées des grains sont déjà des données des nombres quantiques différents, et que la position par le chocs est une donnée parmi d’autres, de plus on ne s’adresse pas aux électrons, mais à leurs constituants. Donc médité Monsieur Paris et restez calme, car vous avez totalement le droit de refuser mes petites inventions, car cela n’est jeux de grains, mais qui peut quand même bloquer la machine. Je suis donc désolé pour sûrement vous avoir mis dans état non quantique, mais sûrement un état caustique.
Amicalement.
JFP/Jean-François POULIQUEN.
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 6 février 2019, 12:17, par Robert Paris
Mais justement "interagir par contact", c’est ce qui n’est pas possible entre matières !!! En effet, il est impossible que deux particules réelles suppriment le nuage de polarisation virtuel de chacune d’elle qui les sépare. Ce n’est pas une question de caractériser les thèses de l’autre. C’est un problème physique incontournable !
2. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 7 février 2019, 14:58, par Robert Paris
« un article de ce Pauli exprimant cette impossibilité que la matière puisse s’agglomérer, et bien j’aurai lu, mais là rien de tel » demandez-vous.
Cherchez "principe de Pauli" et vous verrez...
Lire ici
4. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 7 février 2019, 15:02, par Robert Paris
et dites moi quand vous passez à Paris...
5. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 7 février 2019, 22:49, par JFP/Jean-François POULIQUEN.
Bonsoir.
___Comme il y a de l’orage, alors qu’il pleuve un bon coup !!!
___Voir aussi mon commentaire confirmant ce que j’ai compris de l’exclusion de Pauli : :
Qu’est-ce que le principe de Pauli ?
___Est-ce qu’une réaction en chaîne est une interaction par contact ?? Si oui et bien il faut considérer que deux grains qui se percutent et de deux systèmes différents soit une réaction en chaîne mais sans suite, car il n’y a pas de chaîne qui puisse durer faisant boule de neige. Si non pour la réaction en chaîne, alors cela vient de sortir pour ces petits grains et c’est donc une nouveauté encore toute chaude à cause du contact très bref mais définitif qui est comme une explosion et où l’énergie suivant cette belle formule E=Mc2 donne une très grande énergie, mais comme ce grain est très très petit alors l’énergie dégagée est moindre et ce traduit en énergie thermodynamique, donnant un peu de chaleur par rayonnement. Ensuite après explosion comme il manque un élément grain dans chaque système et bien ils seront pris dans ce vide quantique qui est une réserve pour toujours avoir la même quantité de grains pour chaque système. Il faut voir que ce n’est pas deux électrons qui collisionnent mais deux grains de ces électrons, et donc il faut comprendre le rapport de masse par rapport à un neutrino par exemple où la masse du neutrino est de 511/0.0022=232|272 donc si on considère que les grains sont forcément plus petit en masse que l’électron de 232|272 cela nous donne une masse de : :
0,000|913|2×10E−27 kg/( 511/0.0022=242|272)=0,000 000|003769×10E−27 kg= 3,769×10E−36 kg
et si cette masse de vous semble encore très grande et faille supposer et forcément que le neutrino ezst lui meme composé de grains et qui faille encore diviser cette de 10|000 au pif pour nous donner une masse de ce grin élémentaire de : : 3,769×10E−36 kg/10000= 3,769×10E−40 kg et donc nous somme loin de la petite masse de l’électron qui fait : :
0,000|913|2×10E−27 kg. Et en comparaison nous avons une masse de 3,769×10E−40 kg
donc 232|272/10|000=2|322|720|000 et donc plus de deux milliads de fois plus petit que la masse de l’électron qui ne pèse déja pas lourd.
Donc explosion de deux grains ne donnant pas une très grande énergie mais une énergie de chaleur, une énergie de rayonnement, et plus il y a d’explosions plus ca chauffe c’est normal, maintenant pour arrivéer à des plasma, c’est à voir, mais je m’en moque car j’ai une explication pour définir ce qu’est la chaleur au niveau de la matière solide comme liquide sans passer par des gaz, et cela me suffit comme rien de trouvé pour cette chaleur.
Donc que vous soyer pas d’accord et bien trouvez des contres pour me dire que c’est faux, et si le coeur vous en dit, et bien trouvé une solution pour savoir quel est le mécanisme de cette chaleur dans les solides et les liquides sans donner des phrases trop généralisée car la matière ce n’est n’est pas un ensemble mais constituée de petites choses, et si il y a mécanisme et bien faut dire le quel comme les éléments eux memes qui sont en jeux, car les solides ne sont pas des gaz.
___Je respecte l’exclusion de Pauli et vous n’en parlez pas. Y a t-il d’autres machins qui puissent ne pas fonctionner avec ce concept de grains et de collisions de grains appartenantt à des atomes différents ?? De définir une solution n’est pas si facile que cela, maintenat si cette solution ne tient pas la route, alors il faut le démontrer avec de arguments valables. Comme il n’y a pas de mécanisme pour définir la chaleur de solide et liquide, et bien je vous propose d’en définir une.Et que cela soit vrai ou fzux c’est au moins déja un mécanisme et un concept.
Amicalement.
JFP/Jean-François POULIQUEN.
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 8 février 2019, 09:14, par Robert Paris
Qu’est-ce que le principe de Pauli ? C’est l’existence d’une force de répulsion créée par un champ de la particule.
6. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 8 février 2019, 10:42, par JFP/Jean-François POULIQUEN.
Bonjour
___Mercie de votre réponse. Et bien pour moi, la particule ne créer pas un champ, mais le possède constamment. Ce qui veut dire qu’une particule rayonne constamment mais que ce rayonnement ne se dissipe pas, mais est gardé autour où la concentration en grain est plus forte. D’ailleurs comme déjà dit ce grain rayonne au sens où il est flou et émet quelque chose qui revient sur lui, et n’est pas dans cet esprit d’une étoile qui évacue son rayonnement et donc une énergie. Là c’est un rayonnement stationnaire qui n’est pas une onde stationnaire, car ce genre de notion n’existe pas pour moi, mais un mouvement perpétuel où sans cesse des choses parlent et reviennent de ce grain. Comme je parle de grains, et bien forcément à l’échelle supérieur de l’électron par exemple, qui pour vous est un nuage, et bien ce nuage est l’ensemble des rayonnements de ses grains, et plus on s’éloigne de centre de l’électron et moins il rayonne, car la densité l’affaiblie. Donc pour le redire plus simplement ce nuage est un ensemble de grains internes qui rayonnent localement , mais qui sont stationnaires, et donc ce rayonnement global de l’électron est flou et plus en s’éloigne d’un centre fictif, et bien moins il y a de grains, et donc plus le rayonnement est faible. La force de répulsion comme vous dites est constante pour moi, et non homogène, car le rayon du rayonnement des grains et l’ensemble des grains s’éparpille, mais plus on va vers le centre de cette structure-champ et plus le rayonnement est intense, car forcément plus de grains...
___Pour le redire il n’y a pas de création de force de répulsion fonction d’éléments ou autres, mais un rayonnement constant et stationnaire mais non uniforme. C’est un état en perpétuel changement et actif mais local. C’est en fait une image très simple où votre nuage comporte de vrais élément très petits et qui rayonnement localement et garde ce rayonnement. Et l’ensemble de ces petits rayonnement constitue le nuage et pour moi une structure-champ.
Amicalement.
JFP/Jean-François POULIQUEN.
7. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 8 février 2019, 10:45, par JFP/Jean-François POULIQUEN.
Dans ce concept de grains, je n’ai que défini la constitution du nuage qui n’existait pas avant.
1. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 8 février 2019, 13:29, par Robert Paris
Il est remarquable qu’après toutes ces discussions, tu restes aussi rétif à l’idée principale largement défendue sur nos deux sites, à savoir qu’il n’existe jamais une particule individuelle, ni un nuage de particules individuelles, mais plusieurs niveaux hiérarchiques emboités de structures, niveaux qui modifient l’expression des lois de la Physique, impliquent même des contradictions entre les images de la réalité au différents niveaux. Par exemple, nous ne pouvons absolument pas dire à quel mouvement nous appartenons : nous tournons avec la Terre, avec le Soleil, avec la Galaxie, avec l’amas de galaxies, avec l’amas d’amas !!! Tout ce qui se produit le fait en même temps à toutes les échelles, des plus petites aux plus grandes. Je rajouterai même que l’un des grands progrès de la Physique réalisés par le physicien Lorentz a été de démontrer cela pour le passage du niveau atomique au niveau macroscopique, à propos de l’expression du champ électromagnétique. Pourquoi je ne retiens pas le seul concept de nuage de grains ? Mais parce qu’il y a d’autres niveaux, au dessus et en dessous et il y a tous les passages d’un niveau à l’autre qui sont nécessaires pour comprendre le monde réel. Les nuages de grains en question devraient devenir grains puis devenir nuages de nuages et même nuages de nuages de nuage… de grain ! Tout en restant grains puisque le monde est onde/particule ! Ce qui serait nécessaire, si tu veux que tes efforts de pensée physique, à mon humble point de vue puisque tu me le demandes, mènent à quelque chose d’utile, ce serait de concevoir la même chose avec des de nombreux niveaux hiérarchiques allant du virtuel de virtuel jusqu’au niveau des grandes bulles du vide intergalactique !!! Mais tu risques de trouver qu’un tel effort, c’est seulement du commentaire… Tes propos sont bien plus polémiques que les miens et relèvent des soi-disant contradictions formelles qui ne sont en fait que ton refus des contradictions réelles, celles de la réalité dialectique du monde. Mais ce n’est pas grave : le but n’est pas que l’on tombe d’accord, sinon on n’aurait pas commencé cette discussion. Le but, c’est que chacun progresse dans son propre point de vue et, éventuellement, corrige quelques éléments faibles au sein de notre propre raisonnement. Bien sûr, la vérité est notre seul but mais qui est détenteur de « la vérité », nul ne le sait. Il est certain qu’en Physique, on est dans des difficultés considérables, mon effort ayant surtout consisté non en commentaires comme tu dis gentiment, mais en tentatives d’exprimer « en français », c’est-à-dire par des mots, les problèmes posés et les thèses défendues, afin d’éviter de supprimer les concepts en ne diffusant que des thèses mathématiques. Cela te semble très négligeable visiblement mais cela te permet cependant d’y intervenir même si tu ne disposes pas de tous les grands outils de la Physique et c’est tant mieux.
8. « Comment un observateur se déplaçant à la vitesse de la lumière (aux côtés du photon lumineux) voit-il le monde ? » ou le paradoxe de la relativité restreinte, 13 février 2019, 11:40, par JFP/Jean-François POULIQUEN.
Bonjour.
___Je dois très mal n’exprimer car si vous comprenez "un nuage de particules", cela n’est pas du tout ce que veux exprimer. Si je prend un électron, et peu importe ce qu’il est, et comment il se manifeste, et comment il se divise en niveaux, en couche en ce que vous voulez, et ce sans isoler cet électron, car vous dites que j’isole les particules et bien je n’isole rien du tout, car je le place dans son contexte où il est autour du noyau atomique, et peu importe comment il se comporte et quelle est sa forme et quelle est sa géométrie. Ce que je veux dire c’est que l’on assimile cet électron à quelque chose non clair, qui peut se comporter en tant que corpuscule ou en tant que onde. Cet électron dans son contexte est pour moi, non un objet palpable, mais quelque chose de flou qui se déforme, et sa constitution est fait de choses que j’appelle des grains rayonnants. Donc je redis les mêmes choses, un électron est un ensemble de grains, mais ces grains ne sont pas des billes en dur, mais justement des entités floues et rayonnantes constituant le grain. Je décris donc la consistance de l’électron et non comment il se comporte, comment il se divise, comment il fonctionne... car je décris cet électron en tant que constitution de quelque chose, et cette substance-chose sont des éléments que j’appelle grains. Maintenant les éléments constituant l’électron ne sont pas des billes en dur, mais une structure rayonnante. Si cet électron définit des couches en lui-même, cela ne change rien dans ce que je veux exprimer en tant que constitution. Vous dites que je suis rétif, mais dans la mesure où vous déformer ce que j’écris, change la donne, car vous ne comprenez pas ce que j’essaie d’expliquer. C’est sans doute mon écriture qui n’est pas claire. Mais si je vous demandai de quoi est constitué l’électron ou quelle est sa substance ? Et bien je pense que vous ne pourriez pas me répondre, car on n’en sais rien. Que vous le voyez en oignon ou autre chose cela ne change en rien de savoir de quoi est constitué cet oignon, car présentez sa forme, non définitive d’ailleurs, mais pas de quoi il est fait. Que l’électron définisse des niveaux hiérarchiques d’organisation est une chose mais que ces niveaux soient eux mêmes définis par des grains cela est totalement possible. On pourrai même considérer que n’est pas l’électron qui saute d’un point à un autre, mais ses éléments. De toutes façons que veut dire des niveaux hiérarchique en tant que substance ou entité ??
Amicalement.
JFP/Jean-François POULIQUEN.