Notre point de vue sur ce thème
Chaos déterministe et Philosophie
« Entre le temps et l’éternité » d’Ilya Prigogine et Isabelle Stengers
« Les comportements dynamiques chaotiques permettent de construire ce pont, que Boltzmann n’avait pu créer, entre la dynamique et le monde des processus irréversibles. La nouvelle représentation de l’objet dynamique, non locale et à symétrie temporelle brisée, n’est pas une description approximative, plus pauvre que la représentation classique. Elle (...)
Accueil > 01 - PHILOSOPHIE - PHILOSOPHY > Chapter 09 : The model of deterministic chaos - Le modèle du chaos déterministe
Chapter 09 : The model of deterministic chaos - Le modèle du chaos déterministe

The model of deterministic chaos
Le chaos déterministe, le film

Attracteur étrange : les trajectoires d’un système chaotique suivent des chemins fractals.
L’étude de ce phénomène révèle une surprise majeure : chaos ne rime pas avec désordre, bien au contraire ! Ainsi, le passage d’un état stable à un état chaotique est le même pour n’importe quel système – qu’il s’agisse d’un pendule double ou de la population de lapins sur une ile déserte – et il suit la courbe de la bifurcation vers le chaos (voir image ci-contre). Tout d’abord, le système est stable et toutes les conditions initiales convergent vers une seule solution après un temps suffisamment long, comme la population de lapins qui devient constante. Le système devient ensuite bistable et oscille entre deux solutions, puis le nombre passe à 4, 8, 16, 32, etc., jusqu’à devenir infini : le système est désormais chaotique.
Cette description un peu fastidieuse dévoile la puissance de la notion de chaos et l’origine de la fascination qu’il exerce, car la courbe de la bifurcation vers le chaos est universelle. Peu importe le système, on ne peut l’éviter. Contrairement à la loi de la gravitation, qui ne concerne que l’attraction entre les masses, ou à la mécanique quantique, qui décrit le monde microscopique, la théorie du chaos est la même en sociologie qu’en physique. Cette idée d’universalité a pris une importance considérable depuis la découverte du chaos. Qu’il s’agisse de fractales, de « criticalité auto-organisée », de complexité ou d’émergence, on observe des comportements similaires à de nombreuses échelles de taille (voir illustration), et ceux-ci transcendent les frontières traditionnelles des disciplines. Il reste encore à mettre de l’ordre dans tous ces concepts, à comprendre pleinement leur valeur et, surtout, à poursuivre l’exploration de cette universalité fascinante. La physique du 21e siècle sera probablement d’un grand intérêt pour tous les domaines du savoir !
Normand Mousseau
Voir des attracteurs étranges (courbes qui sont le signal du chaos déterministe)
Des structures fractales, le film

Un exemple d’ondes non-linéaires chaotiques
"Les comportements dynamiques chaotiques permettent de construire ce pont, que Boltzmann n’avait pu créer, entre la dynamique et le monde des processus irréversibles. La nouvelle représentation de l’objet dynamique, non locale et à symétrie temporelle brisée, n’est pas une description approximative, plus pauvre que la représentation classique. Elle définit au contraire cette représentation classique comme relative à un cas particulier. (…) Nous savons aujourd’hui que ces derniers (les systèmes non-chaotiques), qui dominèrent si longtemps l’imagination des physiciens, forment en fait une classe très particulière. (…) C’est en 1892, avec la découverte d’un théorème fondamental par Poincaré ( la loi des trois corps), que se brisa l’image homogène du comportement dynamique : la plupart des systèmes dynamiques, à commencer par le simple système « à trois corps » ne sont pas intégrables."
dans « Entre le temps et l’éternité » d’Ilya Prigogine et Isabelle Stengers

LE NUAGE, STRUCTURE AUTO-ORGANISÉE, DISSIPATIVE ET INSTABLE, INTERFACE DYNAMIQUE ET FRACTALE DES PHASES GLACE, LIQUIDE ET VAPEUR D’EAU DANS L’AIR
« Le type de nuages convectifs connus sous le nom de cumulus sont produits par les vents verticaux qui ont lieu dans des régions d’air chaud et humide, par le principe d’Archimède. Ce soulèvement rapide a comme conséquence l’expansion adiabatique et le refroidissement de l’air, et la formation conséquente de gouttelettes d’eau. Leur distribution irrégulière disperse la lumière du soleil géometriquement dans toutes les directions, produisant l’aspect blanc lumineux typique de la neige, évoluant en nuances de gris de par leur épaisseur optique. Chaque nuage est de vie courte, durant environ 15 minutes en moyenne. »
Tiré de :
1. H. R. Pruppacher, J. D. Klett, “Microphysics of clouds and precipitation“, Springer (1997) ; R. A. Houze, “Cloud Dynamics“, Academic Press (1994)
2. Sarah Robinson, Flow Visualization Course, University of Colorado

LA PARTICULE : UNE FRACTALE
L’électron n’a pas une position fixe : sa charge tremble, sa masse saute d’un point à un autre, son nuage de polarisation interagit avec le voisinage.... Cela définit diverses "dimensions" de l’électron. S’il est capté, il est ponctuel. Sa masse est ponctuelle. Sa charge est ponctuelle. S’il interagit, il est considéré par l’autre objet comme une zone de dimension non nulle. les divers es dimensions ont entre elles un rapport égal à la constante de structure fine alpha. Voilà les résultats de la physique quantique sur la "particule élémentaire".
Qu’est-ce que l’atome, l’élémentaire, l’ « insécable » ? Un nuage de points à de nombreuses échelles !

UN SEUL NEURONE EST DÉJÀ UNE ARBORESCENCE FRACTALE
"L’étude de phénomènes électriques communs également à tous les neurones, à l’aide de la dynamique non linéaire mise au point par les physiciens, a d’autre part suggéré que l’apparence stochastique de ces processus cache en fait un ordre sous-jacent, celui du chaos déterministe. Le terme "déterministe" signifiant que la dynamique en cause obéit bien à des lois mais, que l’évolution des phénomènes concernés est imprévisible du fait de leur sensibilité à toute perturbation."
Henri Korn
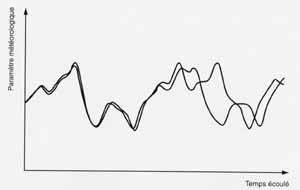
LA "SENSIBILITÉ AUX CONDITIONS INITIALES" SIGNIFIE QUE LES LOIS NE PERMETTENT PAS DE PRÉDIRE PARCE QU’UN TOUT PETIT CHANGEMENT DES VALEURS DE DÉPART ENTRAINE UN AVENIR TRÈS DIFFÉRENT
Quand Henri Poincaré inventait le chaos déterministe
Dans « Sciences et méthode » :
« Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir et alors nous disons que cet effet est dû au hasard. Si nous connaissons exactement les lois de la nature et la situation de ce même Univers à l’instant initial, nous pourrions prédire exactement la situation de ce même Univers à un instant ultérieur. Mais, lors même que les lois naturelles n’auraient plus de secret pour nous, nous ne pourrions connaître la situation initiale qu’approximativement. Si cela nous permet de prévoir la situation ultérieure avec la même approximation, c’est tout ce qu’il nous faut, nous disons que le phénomène a été prévu. Il peut arriver que des petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons un phénomène fortuit. »
Le chaos déterministe, ni ordre, ni désordre,
Un monde dynamique non-linéaire aux frontières fractales



FRACTALES DE JULIA ET DE MANDELBROT
Mots clefs :
dialectique –
discontinuité –
physique quantique – relativité –
chaos déterministe – percolation –
système dynamique –
non-linéarité –
émergence –
inhibition –
boucle de rétroaction –
contradictions –
crise –
transition de phase –
auto-organisation –
Blanqui -
Trotsky –
Prigogine - la révolution

FRONTIÈRE FRACTALE DANS UN PROCESSUS DE DIFFUSION

MOUVEMENT BROWNIEN
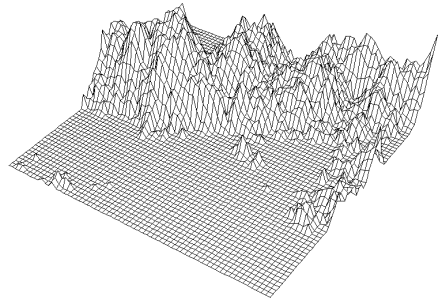
UNE MONTAGNE REPRÉSENTÉE PAR UNE FONCTION FRACTALE

PHOTO DE FOUGÈRE NATURELLE ET IMAGE DE FOUGÈRE PRODUITE PAR UNE FONCTION FRACTALE
« Je ne parviens pas à me défendre de la conviction que ces fougères fausses avertissent l’esprit qu’il est de plus vastes lois qui gouvernent en même temps l’inerte et l’organique. »
Vincent Fleury
dans « Arbres de pierre » ou « La croissance fractale de la matière »
